Question

A projectile is fired from ground level at an angle above the horizontal on an airless planet where g = 10.0 m/s2. The initial x and y components of its velocity are 86.6 m/s and 50.0 m/s respectively. How long after firing does it take before the projectile hits the level ground?

Answer 1

10 s

Step-by-step explanation:

We are given that

`g=10.0m/s^2`

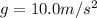
Initially

`v_x=86.6m/s,y=50.0m/s`

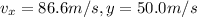
We have to find the time after firing taken by projectile before it hits the level ground.

v=
`√(v^2_x+v^2_y)`

`v=√((86.6)^2+(50)^2)=99.99 m/s`

`\theta=tan^(-1)((v_x)/(v_y))`

`\theta=tan^(-1)((50)/(86.6))=30^(\circ)`

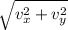
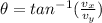
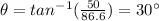
Now,

`t=(vsin\theta)/(g)`

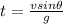
Using the formula

`t=(99.99sin30)/(10)`

`t=4.99\approx 5 s`

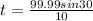
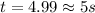
Now, total time,T=2t=
`2* 5=10s`

Hence, after firing it takes 10 s before the projectile hits the level ground.