Question

The expected duration of the project (average) is 30 days and variance is 16. 1. What is the probability that the project will be completed on day 32 or earlier? 2. Suppose the official deadline for the project is 34 days. What is the probability that the project will be delayed?

Answer 1

1. 69.15% probability that the project will be completed on day 32 or earlier

2. 15.87% probability that the project will be delayed

Explanation:

Problems of normally distributed samples are solved using the z-score formula.

In a set with mean
`\mu` and standard deviation(which is the square root of the variance)
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

In this question, we have that:

`\mu = 30, \sigma = √(16) = 4`

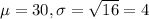
1. What is the probability that the project will be completed on day 32 or earlier?

This is the pvalue of Z when X = 32. So

`Z = (X - \mu)/(\sigma)`

`Z = (32 - 30)/(4)`

`Z = 0.5`

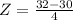
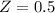
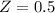`Z = 0.5` has a pvalue of 0.6915

69.15% probability that the project will be completed on day 32 or earlier

2. Suppose the official deadline for the project is 34 days. What is the probability that the project will be delayed?

This is 1 subtracted by the pvalue of Z when X = 34. So

`Z = (X - \mu)/(\sigma)`

`Z = (34 - 30)/(4)`

`Z = 1`

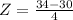
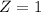
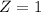`Z = 1` has a pvalue of 0.8413

1 - 0.8413 = 0.1587

15.87% probability that the project will be delayed