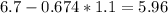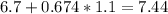Question

Engineers must consider the breadths of male heads when designing helmets. The company researchers have determined that the population of potential clientele have head breadths that are normally distributed with a mean of 6.7-in and a standard deviation of 1.1-in.In what range would you expect to find the middle 50% of most head breadths

Answer 1

`6.7 -0.674 *1.1 =5.96`

`6.7 +0.674 *1.1 =7.44`

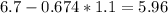
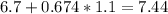
Explanation:

Let X the random variable that represent the head breadths of a population, and for this case we know the distribution for X is given by:

`X \sim N(6.7,1.1)`

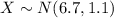
Where
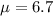`\mu=6.7` and
`\sigma=1.1`

We want the range of the middle 50% values on the distribution. Since the normal distribution is symmetrical we know that in the tails we need to have the other 50% and on each tail 25% by symmetry.

We can use the z score formula given by:

`z=(x-\mu)/(\sigma)`

The critical values that accumulates 0.25 of the area on each tail we got:

`z_(crit)= \pm 0.674`

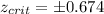
And if we solve x from the z score we got:

`x = \mu \pm z \sigma`

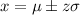
And replacing we got:

`6.7 -0.674 *1.1 =5.96`

`6.7 +0.674 *1.1 =7.44`