Question

Assume a 10-year period at 8% compounded continuously and find the following: (a) the present value; (b) the accumulated amount of money flow at t = 10.

f(t)= 400e^0.03t

Answer 1

Explanation:

Consider the function of the rate of flow of money in dollar per year is

`f(t)= 400e^(0.03t)`

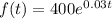
The objective is to find the present value of this income over 10 years period an assume an annual interest rate of 8% compounded continuously.

Given that,

`f(t)= 400e^(0.03t)`

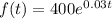
r = 0.08, t = 10

if f(t) is the rate of continuously money flow at an interest rate r to T year,

the present value is,

`P= \int\limits^T_0 {f}(t)e^(-rt) \, dt`

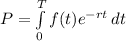
Now input the values to get

`p=\int\limits^(10)_0 400e^(0.03t)*e^(-0.08t) dt`

`=400\int\limits^(10)_0 e^(0.03t)*^(-0.08t) dt`

`= 400\int\limits^(10)_0 e^(-0.05t) dt`

`=400(-(e^(-0.05t))/(0.05) )|_0^1^0`

`=-(400)/(0.05) (e^(-0.05*10)-e^(-0.05*0))\\\\=-(400)/(0.05) (e^(-0.5)-e^(*0))\\\\=3147.75`

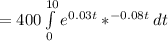
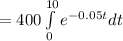
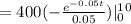
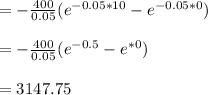
Therefore, the present value is $3147.75