Question

The planet Earth travels in a circular orbit at constant speed around the Sun. What is the net work done on the Earth by the gravitational attraction between it and the Sun in one complete orbit

Answer 1

WT = 3.32*10^34 J

Step-by-step explanation:

The work done by the gravitational attraction between the Sun and the Earth in one complete orbit of the Earth can be calculated by using the following formula:

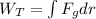`W_T=\int F_g dr` (1)

Fg: gravitational force between Sun and Earth

The gravitational force is given by:

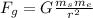`F_g=G(m_sm_e)/(r^2)` (2)

G: Cavendish's constant = 6.674*10^-11 m^3 kg^-1 s^-2

ms: mass of the sun = 1.989*10^30 kg

me: mass of the Earth = 5.972 × 10^24 kg

r: distance between Earth and Sun, this value is a constant r = R = 149,597,870 km

You replace the formula (2) in (1):

`W_T=\int G(m_sm_e)/(R^2)dr=G(m_sm_e)/(R^2)\int dr\\\\W_T=G(m_sm_e)/(R^2)(2\pi R)=2\pi G(m_sm_e)/(R)`

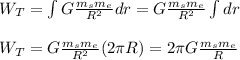
Next, you replace the values of all variables and solve obtain WT:

`W_T=2\pi (6.674*10^(-11)m^3kg^(-1)s^(-2))((1.989*10^(30)kg)(5.972*10^(24)kg))/((149597870*10^3 m))\\\\W_T=3.32*10^(34)J`

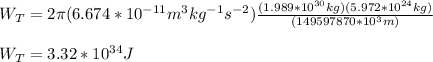
hence, the work done on the Earth, in one orbit, is 3.32*10^34 J