Question

Find the largest interval which includes x = 0 for which the given initial-value problem has a unique solution. (Enter your answer using interval notation.) (x − 5)y'' + 3y = x, y(0) = 0, y'(0) = 1

Answer 1

The largest interval is
`-\infty < 0 < 5`

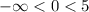
Explanation:

From the question the equation given is

`(x-5)y'' + 3y = x \ \ \ y(0) = 0 \ , y'(0) = 1`

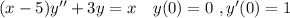
Now dividing the both sides of this equation by (x-5)

`y'' + (3y)/((x-5)) = (x)/(x-5)`

Comparing this equation with the standard form of 2nd degree differential which is

`y'' + P(x)y' + Q(x) y = R(x)`

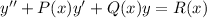
We see that

`Q(x) = (3y)/((x-5))`

`R(x) = (x)/((x-5))`

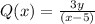
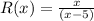
So at x = 5
`Q(x) \ and \ R(x)` are defined for this equation because from the equation of
`Q(x) \ and \ R(x)` x = 5 give infinity

This implies that the largest interval which includes x = 0 , P(x) , Q(x) , R(x ) is

`-\infty < 0 < 5`

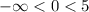
This because x = 5 is not defined in y domain