Question

A project team assesses their primary risk factor's probability of failure with a maturity risk of 0.3, a complexity risk of 0.7, and a dependency risk of 0.8. The probability of failure is:

a. Greater than 0.3 but less than or equal to 0.55.
b. Greater than or equal to 0.9.
c. Greater than 0.56 but less than or equal to 0.89.
d. Less than or equal to 0.3.

Answer 1

b. Greater than or equal to 0.9.

Explanation:

We have three types of risks, that can make the project fail independently.

The probability of failure have to be calculated as the complement of the probability of success, and the probability of success is the probability of avoiding each of the risks.

The probability of avoiding each of the risks is the complementary probability of each risk. For example, the probability of avoiding the maturity risk (0.3) is 1-0.3=0.7.

Then, we can calculate the probabilty of success as:

`P_s=(1-P_(mr))(1-P_(cr))(1-P_(dr))\\\\P_s=(1-0.3)(1-0.7)(1-0.8)\\\\P_s=0.7\cdot 0.3\cdot 0.2\\\\P_s=0.042`

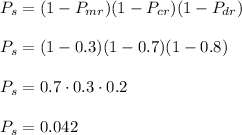
Then, the probability of failure is the complementary of the probability of success:

`P_f=1-P_s\\\\P_f=1-0.042=0.958`

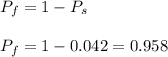
The probability of failure is Pf=0.958