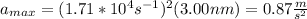Question

The displacement of the air molecules in a sound wave is modeled with the wave function s(x, t) = 3.00 nm cos(50.00 m−1x − 1.71 ✕ 104 s−1t). (a) What is the wave speed (in m/s) of the sound wave? 342 Correct: Your answer is correct. m/s (b) What is the maximum speed (in m/s) of the air molecules as they oscillate in simple harmonic motion? m/s (c) What is the magnitude of the maximum acceleration (in m/s2) of the air molecules as they oscillate in simple harmonic motion?

Answer 1

a) 342 m/s

b) 51*10^-6 m/s

c) 0.87m/s^2

Step-by-step explanation:

The following function describes the displacement of the molecules in a sound wave:

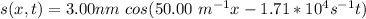`s(x,t)=3.00nm\ cos(50.00\ m^(-1)x-1.71*10^4s^(-1)t)` (1)

The general form of a function that describes the same situation is:

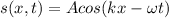`s(x,t)=Acos(kx-\omega t)` (2)

By comparing equations (1) and (2) you have:

k: wave number = 50.00 m^-1

w: angular frequency = 1.71*10^4 s^-1

A: amplitude of the oscillation = 3.00nm

a) The speed of the sound is obtained by using the formula:

`v=(\omega)/(k)=(1.71*10^4s^-1)/(50.00m^(-1))=342(m)/(s)`

b) The maximum speed of the molecules is the maximum value of the derivative of s(x,t), in time. Then, you first obtain the derivative:

`(ds)/(st)=-\omega A sin(kx-\omega t)`

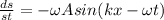
The max value is:

`v_(max)=\omega A`

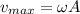
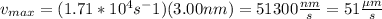`v_(max)=(1.71*10^4s^-1)(3.00nm)=51300(nm)/(s)=51(\mu m)/(s)` = 51*10^-6 m/s

c) The acceleration is the max value of the derivative of the speed, that is, the second derivative of the displacement s(x,t):

`a=(dv)/(dt)=(d^2s)/(dt^2)=-\omega^2A cos(kx-\omega t)\\\\a_(max)=\omega^2 A`

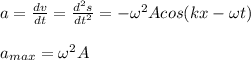
Then, the maximum acceleration is:

`a_(max)=(1.71*10^4s^(-1))^2(3.00nm)=0.87(m)/(s^2)`