Question

An equation of an ellipse is given. x2 16 + y2 25 = 1 (a) Find the vertices, foci, and eccentricity of the ellipse. vertex (x, y) = 0,−5 (smaller y-value) vertex (x, y) = 0,5 (larger y-value) focus (x, y) = 0,−3 (smaller y-value) focus (x, y) = 0,3 (larger y-value) eccentricity 3 5​ (b) Determine the length of the major axis.

Answer 1

(a)

• The vertices are at (0,-5) and (0,5).
• The coordinates of the foci are (0,-3) and (0,3).
• Eccentricity=3/5

(b)Length of the major axis=10

Explanation:

When the major axis of an ellipse is parallel to the y-axis.The standard form of the equation of an ellipse is given as:

`(x^2)/(b^2)+(y^2)/(a^2)=1`

Given the equation:

`(x^2)/(16)+(y^2)/(25)=1`

(I)The coordinates of the vertices are
`(0, \pm a)`

`a^2=25\\a^2=5^2\\a=5`

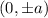
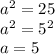
Therefore, the vertices are at (0,-5) and (0,5).

(II)The coordinates of the foci are
`(0, \pm c)$ where c^2=a^2-b^2`

`c^2=a^2-b^2\\c^2=25-16\\c^2=9\\c=3`

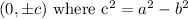
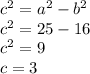
The coordinates of the foci are (0,-3) and (0,3).

(III)Eccentricity

This is the ratio of the distance c between the center of the ellipse and each focus to the length of the semi major axis.

Simply put, Eccentricity =c/a

Eccentricity=3/5

(b)Length of the major axis

The length of the major axis=2a

=2(5)=10.