Answer:
(a) The sample sizes are 6787.
(b) The sample sizes are 6666.
Explanation:
(a)
The information provided is:
Confidence level = 98%
MOE = 0.02
n₁ = n₂ = n
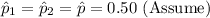
Compute the sample sizes as follows:
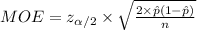
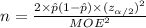

Thus, the sample sizes are 6787.
(b)
Now it is provided that:
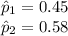
Compute the sample size as follows:
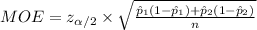
![n=((z_(\alpha/2))^(2)* [\hat p_(1)(1-\hat p_(1))+\hat p_(2)(1-\hat p_(2))])/(MOE^(2))](https://img.qammunity.org/2021/formulas/mathematics/college/jk578kz2fm1ipx9u7wsvq601fxc9sbpqca.png)
![=(2.33^(2)* [0.45(1-0.45)+0.58(1-0.58)])/(0.02^(2))\\\\=6665.331975\\\\\approx 6666](https://img.qammunity.org/2021/formulas/mathematics/college/y08g48jzanqu6n4zjw9fxqfhk6jx24gudp.png)
Thus, the sample sizes are 6666.