Answer:
Probability that 100 or fewer of these Americans could only converse in one language is 0.8599.
Explanation:
We are given that a recent study reported that 73% of Americans could only converse in one language.
A random sample of 130 Americans was randomly selected.
Let
 = sample proportion of Americans who could only converse in one language.
= sample proportion of Americans who could only converse in one language.
The z score probability distribution for sample proportion is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where, p = population proportion of Americans who could only converse in one language = 73%
 = sample proportion =
= sample proportion =
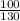 = 0.77
= 0.77
n = sample of Americans = 130
Now, probability that 100 or fewer of these Americans could only converse in one language is given by = P(

 0.77)
0.77)
P(

 0.77) = P(
0.77) = P(


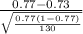 ) = P(Z
) = P(Z
 1.08) = 0.8599
1.08) = 0.8599
The above probability is calculated by looking at the value of x = 1.08 in the z table which has an area of 0.8599.