Answer:
Probability that 32 or more from this sample used Internet Explorer as their browser is 0.9015.
Explanation:
We are given that according to Net Market Share, Microsoft's Internet Explorer browser has 53.4% of the global market.
A random sample of 70 users was selected.
Let
 = sample proportion of users who used Internet Explorer as their browser.
= sample proportion of users who used Internet Explorer as their browser.
The z score probability distribution for sample proportion is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where, p = population proportion of users who use internet explorer = 53.4%
 = sample proportion =
= sample proportion =
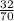 = 0.457
= 0.457
n = sample of users = 70
Now, probability that 32 or more from this sample used Internet Explorer as their browser is given by = P(

 0.457)
0.457)
P(

 0.457) = P(
0.457) = P(


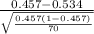 ) = P(Z
) = P(Z
 -1.29)
-1.29)
= P(Z
 1.29) = 0.9015
1.29) = 0.9015
The above probability is calculated by looking at the value of x = 1.29 in the z table which has an area of 0.9015.