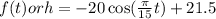Answer:
Explanation:
Let y = -A cos B(t -c) + D
A, amplitude = 20ft
Period = 2π / B ( B = π / 15)
= 30
c = 0
Vertical shift D = 21.5 ft
Equation becomes
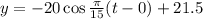
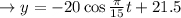
a) Top of the ferris wheel is
t = 15sec, 45sec, height = 41.5ft
b) At the bottom of the ferris wheel
t = 0, 30sec, 60 sec
height = 1.5ft
c) Exact middle of the ferris wheel
t = 15/ 2 = 7.5sec, 22.5sec, 37.5sec, 52.5sec
d)