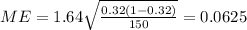Question

Verizon Wireless would like to estimate the proportion of households that use cell phones for their phone service without a land line. A random sample of 150 households was selected and 48 relied strictly on cell phones for their service. The margin of error for a 90% confidence interval for the proportion based on this sample is ________.

Answer 1

`ME = 1.64 \sqrt{(0.32 (1-0.32))/(150)}= 0.0625`

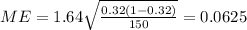
Explanation:

For this case we have the following info given:

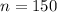`n = 150` represent the sampel size selected

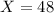`X = 48` represent the number of households who relied strictly on cell phones for their service

The estimated proportion of households who relied strictly on cell phones for their service is given by:

`\hat p =(X)/(n)= (48)/(150)= 0.32`

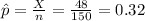
And the margin of error would be given by:

`ME = z_(\alpha/2) √(\hat p(1-\hat p)){n}`

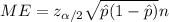
The confidence is 90% so then the significance is
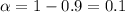`\alpha=1-0.9=0.1` and
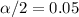`\alpha/2 =0.05` the critical value for this case from the normal standard distribution is:

`z_(\alpha/2)= 1.64`

And the margin of error would be:

`ME = 1.64 \sqrt{(0.32 (1-0.32))/(150)}= 0.0625`