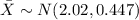Question

The distribution of the amount of change in UF student's pockets has an average of 2.02 dollars and a standard deviation of 3.00 dollars. Suppose that a random sample of 45 UF students was taken and each was asked to count the change in their pocket. The sampling distribution of the sample mean amount of change in students pockets is

Answer 1

`\bar X \sim N (\mu ,(\sigma)/(√(n)))`

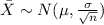
Then the mean would be:

`\mu_(\bar X)= 2.02`

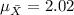
And the deviation:

`\sigma_(\bar X)= (3.00)/(√(45))= 0.447`

And the distribution would be given by:

`\bar X \sim N(2.02, 0.447)`

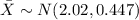
Explanation:

For this case we can define the variable of interest X as the amount of change in UF student's pockets and we know the following parameters:

`\mu = 2.02, \sigma =3.00`

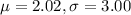
And we select a sample of n=45. Since this sample size is higher than 30 we can apply the central limit theorem and the distirbution for the sample size would be given by:

`\bar X \sim N (\mu ,(\sigma)/(√(n)))`

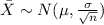
Then the mean would be:

`\mu_(\bar X)= 2.02`

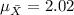
And the deviation:

`\sigma_(\bar X)= (3.00)/(√(45))= 0.447`

And the distribution would be given by:

`\bar X \sim N(2.02, 0.447)`