Question

1. (a) The life time of a certain brand of bulbs produced by a company is normally distributed, with mean 210 hours and standard deviation 56 hours. What is the probability that a bulb picked at random from this company’s products will have a life time of:

(i) (ii) (iii) at least 300 hours,
at most 100 hours, between 150 and 250 hours.
(b) In a contest, two friends, Kofi and Mensah were asked to solve a problem. The probability that Kofi will solve it correctly is and the probability that Mensah
will solve it correctly is . Find the probability that neither of them solved it correctly.
2. Suppose that the random variable, X, is a number on the biased die and the p.d.f. of X is as shown below;
X
1
2
3
4
5
6

P(X=x)
1/6
1/6
1/5
k
1/5
1/6

a) Find;
(i) (ii) (iii) (iv) (v) the value of k. E(X)
E(X2) Var(X) P(1 £X <5)
b) If events A and B are such that they are independent, and P(A) = 0.3 with P(B) = 0.5;
i. ii. Find P(A n B) and P(AUB)
Are A and B mutually exclusive? Explain.
c) In how many ways can the letters of the word STATISTICS be arranged?

Answer 1

See explanation

Explanation:

Q1)a

- Denote a random variable ( X ) as the life time of a brand of bulb produced.

- The given mean ( μ ) = 210 hrs and standard deviation ( σ ) = 56 hrs. The distribution is symbolized as follows:

X ~ Norm ( 210 , 56^2 )

i) The bulb picked to have a life time of at least 300 hours.

- We will first standardize the limiting value of the RV ( X ) and determine the corresponding Z-score value:

P ( X ≥ x ) = P ( Z ≥ ( x - μ ) / σ )

P ( X ≥ 300 ) = P ( Z ≥ ( 300 - 210 ) / 56 )

P ( X ≥ 300 ) = P ( Z ≥ 1.607 )

- Use the standard normal look-up table for limiting value of Z-score:

P ( X ≥ 300 ) = P ( Z ≥ 1.607 ) = 0.054 .. Answer

ii) The bulb picked to have a life time of at most 100 hours.

- We will first standardize the limiting value of the RV ( X ) and determine the corresponding Z-score value:

P ( X ≤ x ) = P ( Z ≤ ( x - μ ) / σ )

P ( X ≤ 100 ) = P ( Z ≤ ( 100 - 210 ) / 56 )

P ( X ≤ 100 ) = P ( Z ≤ -1.9643 )

- Use the standard normal look-up table for limiting value of Z-score:

P ( X ≤ 100 ) = P ( Z ≤ -1.9643 ) = 0.0247 .. Answer

iii) The bulb picked to have a life time of between 150 and 250 hours.

- We will first standardize the limiting value of the RV ( X ) and determine the corresponding Z-score value:

P ( x1 ≤ X ≤ x2 ) = P ( ( x1 - μ ) / σ ≤ Z ≤ ( x2 - μ ) / σ )

P ( 150 ≤ X ≤ 250 ) = P ( ( 150 - 210 ) / 56 ≤ Z ≤ ( 250 - 210 ) / 56 )

P ( 150 ≤ X ≤ 250 ) = P ( -1.0714 ≤ Z ≤ 0.71428 )

- Use the standard normal look-up table for limiting value of Z-score:

P ( 150 ≤ X ≤ 250 ) = P ( -1.0714 ≤ Z ≤ 0.71428 ) = 0.6205 .. Answer

Q1)b

- Denote event (A) : Kofi solves the problem correctly. Then the probability of him answering successfully is:

p ( A ) = 0.25

- Denote event (B) : Menesh solves the problem correctly. Then the probability of him answering successfully is:

p ( B ) = 0.4

- The probability that neither of them answer the question correctly is defined by a combination of both events ( A & B ). The two events are independent.

- So for independent events the required probability can be stated as:

p ( A' & B' ) = p ( A' ) * p ( B' )

p ( A' & B' ) = [ 1 - p ( A ) ] * [ 1 - p ( B ) ]

p ( A' & B' ) = [ 1 - 0.25 ] * [ 1 - 0.4 ]

p ( A' & B' ) = 0.45 ... Answer

Q2)a

- A discrete random variable X: defines the probability of getting each number on a biased die.

- From the law of total occurrences. The sum of probability of all possible outcomes is always equal to 1.

∑ p ( X = xi ) = 1

p ( X = 1 ) + p ( X = 2 ) + p ( X = 3 ) + p ( X = 4 ) + p ( X = 5 ) + p ( X = 6 )

1/6 + 1/6 + 1/5 + k + 1/5 + 1/6 = 1

k = 0.1 ... Answer

- The expected value E ( X ) or mean value for the discrete distribution is determined from the following formula:

E ( X ) = ∑ p ( X = xi ) . xi

E ( X ) = (1/6)*1 + (1/6)*2 + (1/5)*3 + (0.1)*4 + (1/5)*5 + (1/6)*6

E ( X ) = 3.5 .. Answer

- The expected-square value E ( X^2 ) or squared-mean value for the discrete distribution is determined from the following formula:

E ( X^2 ) = ∑ p ( X = xi ) . xi^2

E ( X^2 ) = (1/6)*1 + (1/6)*4 + (1/5)*9 + (0.1)*16 + (1/5)*25 + (1/6)*36

E ( X^2 ) = 15.233 .. Answer

- The variance of the discrete random distribution for the variable X can be determined from:

Var ( X ) = E ( X^2 ) - [ E ( X ) ] ^2

Var ( X ) = 15.2333 - [ 3.5 ] ^2

Var ( X ) = 2.9833 ... Answer

- The cumulative probability of getting any number between 1 and 5 can be determined from the sum:

P ( 1 < X < 5 ) = P ( X = 2 ) + P ( X = 3 ) + P ( X = 4 )

P ( 1 < X < 5 ) = 1/6 + 1/5 + 0.1

P ( 1 < X < 5 ) = 0.467 ... Answer

Q2)b

- Two independent events are defined by their probabilities as follows:

p ( A ) = 0.3 and p ( B ) = 0.5

- The occurrences of either event does not change alter or affect the occurrences of the other event; hence, independent.

- For the two events to occur simultaneously at the same time:

p ( A & B ) = p ( A )* p ( B )

p ( A & B ) = 0.3*0.5

p ( A & B ) = 0.15 ... Answer

- For either of the events to occur but not both. From the comparatively law of two independent events A and B we have:

p ( A U B ) = p ( A ) + p ( B ) - 2*p ( A & B )

p ( A U B ) = 0.3 + 0.5 - 2*0.15

p ( A U B ) = 0.5 ... Answer

- Two mutually exclusive events can-not occur simultaneously; hence, the two events are not mutually exclusive because:

p ( A & B ) = 0.15 ≠ 0

Q2)c

- The letters of the word given are to be arranged in number of different ways as follows:

STATISTICS

- Number of each letters:

S : 3

T : 3

A: 1

I: 2

C: 1

- 10 letters can be arranged in 10! ways.

- However, the letters ( S and T and I ) are repeated. So the number of permutations must be discounted by the number of each letter is repeated as follows:

`(10!)/(3!3!2!) = (3628800)/(72) = 50,400`

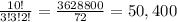
- So the total number of ways the word " STATISTICS " can be re-arranged is 50,400 without repetitions.