Question

At the Laika Boss Kennel Club, there are 15 dogs that are hairy or small, 2 dogs that are hairy and small, and 9 dogs that are small. How many dogs are hairy?

Answer 1

There are 8 number of hairy dogs.

Explanation:

It is given that:

Number of small dogs (Let it be
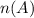`n(A)`) = 9

To find:

Number of hairy dogs (Let it be
`n(B)`) = ?

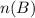Also given the following things:

Number of hairy or small dogs (
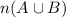`n(A \cup B)`) = 15

Number of hairy and small dogs(both) (
`n(A \cap B)`) = 2

We can use the following formula:

`n(A \cup B) = n(A) + n(B) - n(A \cap B)`

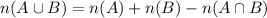
To find
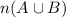`n(A \cup B)`, We have to subtract
`n(A \cap B)` once because
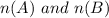`n(A) \ and \ n(B)` both contain the common part and it gets added twice. So, it is subtracted once.

Putting the values in above formula:

`\Rightarrow 15 = 9 + n(B) - 2\\\Rightarrow n(B) = 15 - 7\\\Rightarrow n(B) = 8`

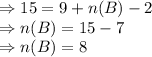
Hence, the number of hairy dogs are 8.