Question

16.

A soccer team has 11 players on the field at the end of a scoreless game. According to league

coach must select 5 of the players and designate an order in which they will take penalty

game. According to league rules, the

(a) Is this a permutation or a combination? Why?

(b) How many different ways are there for the coach to do this?

Answer 1

B

Explanation:

Answer 2

a) Permutation, because the coach has to designate an order in which they will take penalty

b) There are 55,440 different ways for the coach to do this.

Explanation:

It the order is not important, we have a combination.

If the order is important, we have a permutation.

In this question:

5 players from a set of 11 and designate an order.

This means that the order is important, and we have a permutation.

Permutations formula:

The number of possible permutations of x elements from a set of n elements is given by the following formula:

`P_((n,x)) = (n!)/((n-x)!)`

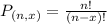
(a) Is this a permutation or a combination? Why?

Permutation, because the coach has to designate an order in which they will take penalty

(b) How many different ways are there for the coach to do this?

`P_((11,5)) = (11!)/((11-5)!) = 55440`

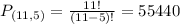
There are 55,440 different ways for the coach to do this.