Question

2.

The Parkside Packing Company needs a rectangular shipping box. The box must have a length

of 11 inches and a width of 8 inches. Find, to the nearest tenth of an inch, the minimum height

of the box such that the volume is at least 800 cubic inches.

(3 points)

Answer 1

9.1 Inches

Explanation:

Length of the proposed box=11 Inches

Width of the proposed box=8 Inches

Required Volume,
`V \geq 800 $ cubic inches.`

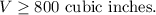
Volume of a Rectangular Prism =Length X Width X Height

Therefore:

`800\\11*8*Height\geq 800\\88*Height \geq 800\\$Divide both sides by 88\\Height \geq 800 / 88\\Height \geq 9.\overline{09}$ inches`

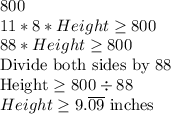
Therefore, the minimum height to the nearest tenth of an inch is 9.1 Inches.