Question

1.Segments AB, EF, and CD intersect at point C, and angle ACD is a right angle. Find the value of g. Do NOT include degrees.

2.Find the area of the unshaded part of the figure
3. In the figure, angles c and e are vertical angles. Angles a and c are complementary angles. The measure of angle d is 124 degrees and the measure of angle c is 56 degrees.

Answer 1

See below;

Explanation:

1 . Consider the step below;

`m< DCA = 90 degrees - Given ,\\m< ACB = 180 degrees - Straight < ,\\\\m< DCA + m< DCB = 180,\\m< DCB = 90 degrees,\\\\By Parts Whole Postulate - m< DCB = m< DCE + m< ECB,\\m< DCB = m< DCE + m< ECB,\\90 = 53 + g,\\Conclusion ; ( g = 37 degrees )`

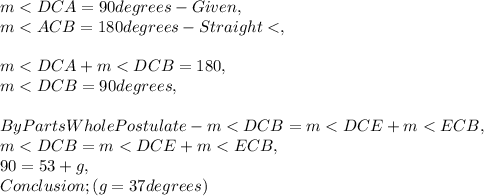
Thus, Solution ; g = 37 degrees

2 . Knowing that these circle are " circumscribed " in this rectangle so that they are perfectly aligned, considering the length of this rectangle to be 20 inches, let us determine the radius;

`Diameter Of 1 Circle - ( 20 inches ) / 4 = 5 inches,\\Radius of 1 Circle = ( 5 inches ) / 2 = 2.5 inches,\\\\Area of 1 Circle = \pi r^2 = \pi * ( 2.5 )^2 = 6.25\pi,\\Area of 4 Circles = 6.25\pi * 4 = 25\pi,\\Area of 4 Circles = Area of Shaded Region,\\\\Conclusion ; Area of Shaded Region = 25\pi`

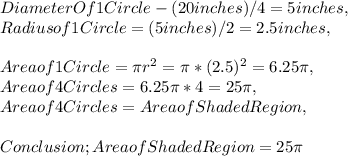
Thus, Solution ; 25π

3. Let us first consider the given, then solve for the value of a, b, e;

`Angles c + e - Vertical Angles,\\Angles a + c - Complementary,\\( a + c ) = 90,\\Angle c = 56 degrees,\\a + 56 = 90,\\Conclusion ; a = 34 degrees,\\\\`

`m< e = m< c,\\Conclusion ; e = 56 degrees`

`m< e + m< a + m< b = 180 - Straight Line,\\56 + 34 + m< b = 180,\\m< b = 180 - 56 - 34,\\Conclusion ; b = 90 degrees`

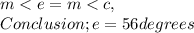
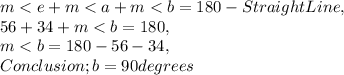
Solution; a = 34°, b = 90°, e = 56°