Answer:
Radius of the circle is 15 inches.
Explanation:
Relation between length of arc, radius and the angle subtended by the arc on center is:
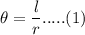
where
 is the central angle in radians subtended by arc
is the central angle in radians subtended by arc
 is the length of arc
is the length of arc
 is the radius of arc
is the radius of arc
We are Given the following details:
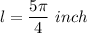
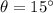
We know that

Converting
 to radians:
to radians:
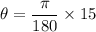 radians
radians
Putting the values of
 and
and
 to find the value of
to find the value of


Hence, Radius of the circle is 15 inches.