Answer:
12(cos120°+isin120°)
Explanation:
The rectangular form of a complex number is expressed as z = x+iy
where the modulus |r| =
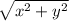 and the argument
and the argument
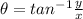
In polar form, x =
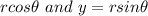

Given the complex number,
 . To express in trigonometric form, we need to get the modulus and argument of the complex number.
. To express in trigonometric form, we need to get the modulus and argument of the complex number.
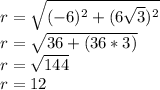
For the argument;
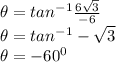
Since tan is negative in the 2nd and 4th quadrant, in the 2nd quadrant,
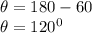
z = 12(cos120°+isin120°)
This gives the required expression.