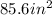Question

What is the surface area of a sphere whose great circle has a circumference of 16.4 inches

Answer 1

`85.6in^2`

Explanation:

to find the surface area we need the radius of the sphere.

We can find the radius using the formula for circumference:

`C=2\pi r`

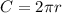
we know that the circumference is

`C=16.4in`

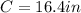
thus

`16.4in=2\pi r`

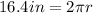
solving for r:

`r=(16.4in)/(2\pi) \\r=2.61in`

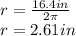
and now that we know the radius we calculate the surface area:

`SA=4\pi r^2`

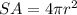
substituting r:

`SA=4\pi(2.61014in)^2\\SA=4\pi(6.81in^2)\\SA=85.6in^2`

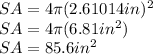
the surface area is equal to
`85.6in^2`