Answer:
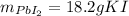
Step-by-step explanation:
Hello,
In this case, the undergoing chemical reaction is:
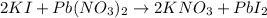
Thus, we proceed to compute the reacting moles of Pb(NO3)2 and KI, by using the given concentrations and densities and molar masses which are 331.2 g/mol and 166 g/mol respectively:
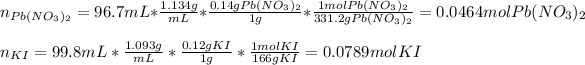
Next, the 0.0464 moles of Pb(NO3)2 will consume the following moles of KI (consider their 1:2 molar ratio):
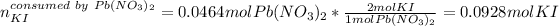
Hence, as only 0.0789 moles of KI are available, KI is the limiting reactant, therefore the formed grams of PbI2, considering its molar mass of 461.01 g/mol and 2:1 molar ratio, are:
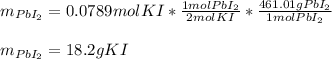
Best regards.