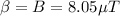Question

Por una espira de 0.5 m2 de área circula una corriente de 5 A. Calcula la densi- dad de flujo magnético B considerando que la espira considera la permeabilidad del medio es la del aire

Answer 1

`\beta=B=8.05\mu T`

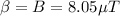
Step-by-step explanation:

The density of the magnetic flux is given by the following formula:

`\beta=(\Phi_B)/(A)=(ABcos\theta)/(A)=Bcos\theta`

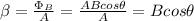
The normal vector A and the vector of the magnitude of the magnetic field are perpendicular, then, the angle is zero:

The magnitude of the magnetic field is calculated by using the formula for B at a distance of x to a point in the plane of the loop:

`B=(\mu_oIR^2)/(2(x^2+R^2)^(3/2))`

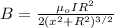
For x = 0 you have:

`B=(\mu_oIR^2)/(2R^3)=(\mu_oI)/(2R)`

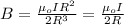
R is the radius of the circular loop and its values is:

`R=\sqrt{(A)/(\pi)}=\sqrt{(0.5m^2)/(\pi)}=0.39m`

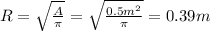
Then, you replace in the equation for B with mu_o = 4\pi*10^-7 T/A:

`B=((4\pi*10^(-7)T/A)(5A))/(2(0.39m))=8.05*10^(-6)T=8.05\mu T`

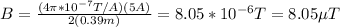
and the density of the magnetic flux is

`\beta=B=8.05\mu T`