Question

Consider the function: f(x) = 2x^2 - 1.5x - 5 and its graph.

If the graph of f(x) is:

(i) first translated 2 units in the positive x direction and 3 units in the positive y

direction

(ii) then, stretched vertically by a factor of 2

(iii) and then reflected across the x-axis

What is the resultant function in standard form and its graph?

Answer 1

f(x) = -4x² + 19x - 18

Explanation:

`f(x) = 2x^2 - 1.5x - 5`

i) If it is translated 2 units in the positive x direction, therefore we use f(x-2)

`y=f(x-2) = 2(x-2)^2 - 1.5(x-2) - 5\\y = 2(x^2-4x+4) - 1.5x+3 - 5\\y=2x^2-8x+8-1.5x+3-5\\y=2x^2-9.5x+6`

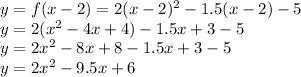
f(x) = 2x² - 9.5x + 6

If it is then translated 3 units in the positive y, we add 3 to the input function to get:

`y=f(x)+3=2x^2-9.5x+6+3\\y = 2x^2-9.5x+9`

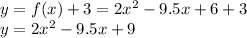
ii) stretched vertically by a factor of 2, we multiply the function by 2 to get:

`y =2( 2x^2-9.5x+9) = 4x^2-19x+18\\y= 4x^2-19x+18`

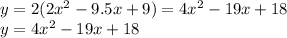
iii) reflected across the x-axis

we multiply the parent function by –1, to get a reflection about the x-axis.

`y= -1(4x^2-19x+18)=-4x^2+19x-18\\y=f(x)=-4x^2+19x-18`