Answer:
The probability of winning a jackpot is
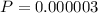
The probability of winning the pick 5 game is
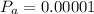
The earning of the lottery organisation if the game were to be runed for no profit is
 $10 000
$10 000
Explanation:
From the question
The sample size is n= 37
The number of selection is
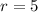
Now the number of way by which these five selection can be made is mathematically represented as
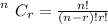
Now substituting values
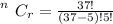
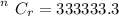
Now the probability of winning a jackpot from any of the way of selecting 5 whole number from 37 is mathematically evaluated as
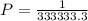
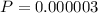
Now the number of ways of selecting 5 whole number from 0 to 9 with repetition is mathematically evaluated as

Now the probability of winning the game is
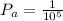
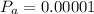
We are told that for a $1 ticket that the pick 5 game returns $50 , 000
Generally the expected value is mathematically represented as

In this question the expected value is $1
So
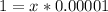
So
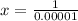
 $10 000
$10 000