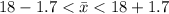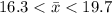Question

A study conducted by Harvard Business School recorded the amount of time CEOs devoted to various activities during the workweek. Meetings were the single largest activity averaging 18 hours per week. Assume that the standard deviation for the time spent in meetings is 5.2 hours. To confirm these results, a random sample of 35 CEOs was selected This sample averaged 16.8 hours per week in meetings. Which of the following statements is correct? A) The interval that contains 95% of the sample means is 16.3 and 19.7 hours. Because the sample mean is between these two values, we have support for the results of the CEO study by the Harvard Business School. B) The interval that contains 95% of the sample means is 17.1 and 18.9 hours. Because the sample mean is not between these two values, we do not have support for the results of the CEO study by the Harvard Business School C) The interval that contains 95% of the sample means is 15.7 and 20.3 hours. Because the sample mean is between these two values, we have support for the results of the CEO study by the Harvard Business School D) The interval that contains 95% of the sample means is 15.7 and 20.3 hours. Because the sample mean is between these two values, we do not have support for the results of the CEO study by the Harvard Business School

Answer 1

The correct option is A

Explanation:

From the question we are told that

The average number of meetings hours per week is
`\mu= 18 \ hours`

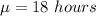
The standard deviation is
`\sigma = 5.2 \ hours`

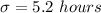
The sample size is n= 35

The sample average per week is
`p = 16.8 \ hours`

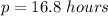
From each solution statement we can deduce that the confidence level is

`t = 95`%

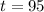Thus the significance level is
`\alpha = 0.05`= 5%

The z value for the significance level is gotten as 1.96 from the z-table

The confidence level interval for the sample mean is mathematically evaluated as

`\= x = \mu \pm (1.96 * (\sigma )/(√(n) ) )`

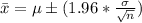
Sustituting values

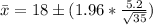
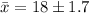
`\= x = 18 \pm (1.96 * (5.2 )/(√(35) ) )`

`\= x = 18 \pm1.7`

=>
`18 - 1.7 < \= x < 18 +1.7`

`16.3 < \= x < 19.7`