The general form for the equation of a line is:
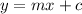
Where:
m is the gradient of the line
c is the y intercept of the line (y - intercept is where the graph crosses the y-axis)
So if you had the following equation:
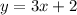
Then:
m = 3
c = 2
So gradient = 3, and y intercept = 2
---------------------------------------------------
Rearranging
So first rearrange both of the equations in the form y = mx + c :
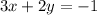 becomes
becomes
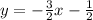
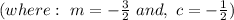
and:
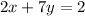 becomes
becomes
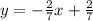

---------------------------------------------
The question tells us that the equation of the line we are looking for has the same y-intercept as:
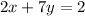
So the line we are trying to work out will also have a y intercept of
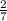
(refer to rearranging)
----------------------------
The question also tells us that the line is perpendicular to
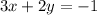
Perpendicular gradient = negative reciprocal of the gradient of the line it is perpendicular to.
So the gradient of the new line will be the negative reciprocal of the gradient of
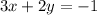
Gradient of
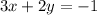 is:
is:
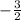
(refer to rearranging)
Gradient of new line: = negative reciprocal of
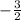 , which is
, which is
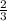
(just flip fraction and change the sign)
------------------------------------
So for the new line:
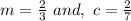
So just substitute in the values for m and c into: y = mx + c
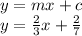
-----------------------------
Answer:
So equation of the new line is:
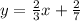
------------
Any questions, just ask.