Answer:
Exact distance =
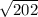
Approximate distance = 14.2127
==========================================================
Work Shown:
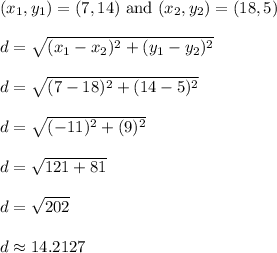
Note: I used the distance formula. Though you could plot the points, form a right triangle, and use the pythagorean theorem as an alternative route. The distance formula is effectively a modified version of the pythagorean theorem.