Question

The drama club at Del Rosa Middle School is having a production.

Tickets cost $3 for students and $5 for adults. A total of 500 tickets
were sold, bringing in $1860. How many of each kind of ticket was
sold?

Answer 1

320 Student Tickets

180 Adult Tickets

Explanation:

You can solve this problem by using system of equations. First, we need to figure out our equations.

Equation 1: x as students and y as adults

`x+y=500`

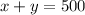
We get this equation because the total tickets sold was 500. The x represents the students sold to students, and the y represents the tickets sold to adults.

Equation 2:

`3x+5y=1850`

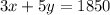
We get this equation based on the prices. Each student ticket costs $3, and each adult ticket costs $5. The total amount earned was $1850.

Now that we have out equations, we can use system of equations to find our students and adults.

`x+y=500`

`3x+5y=1860`

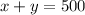
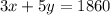
Typically elimination is the easiest strategy because you are able to cross out variables.

`3(x+y=500)`

`3x+5y=1860`

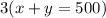
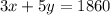
Becomes:

`3x+3y=1500`

`3x+5y=1860`

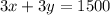
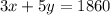
We see that both equations now have 3x. We can cancel out 3x.

`-2y=-360`

`y=180`

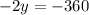
Now that we know y=180, we can plug it back into one of our equations to find x.

`x+180=500`

`x=320`

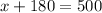
320 student tickets and 180 adult tickets were sold.