Question

Find the approximate perimeter of polygon CODIFYCODIFYC, O, D, I, F, Y plotted below.

Round your final answer to the nearest hundredth.

please helppp

Answer 1

51.53

Explanation:

Answer 2

49.81

Explanation:

the formula I used is distance=
`\sqrt{(x_(2)-x_(1))+(y_(2)-y_(1))}`

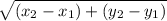
Lets say we are finding the distance from c to y

c=(-6,9)

y=(5,9)

cy=
`\sqrt{(5-(-6))^(2)+(9-9)^2 }`

cy=
`√((11)^2+(0)^2)`

cy=
`√(121+0)`

cy=
`√(121)`

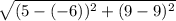
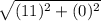
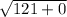
cy=11

And you can find the distance between y and i, i and d, d and o, o and c, using the same formula.

After solving the distance of all I got

yi=16.55294536

id=1

do=9.219544457

oc=12.04159458

After you add them all up you get 49.8140844 which rounded to the nearest hundredth is 48.81.

Thank you and I hope that is helpful.

Sorry that is actually wrong

Check out the other answer.