Question

Which situation gives you the fewest number of possible outcomes?

A.
You choose 2 beads from a jar of 9 beads.
B.
You choose 4 cards out of 8 cards.
C.
You choose 5 people out of 6 people.
D.
You choose 4 socks out of 32 socks in a drawer.

Answer 1

c you choose 5 out of 6 people

Answer 2

1. The situation that gives the fewest number of possible outcomes is option A, where you choose 2 beads from a jar of 9 beads.

Step-by-step explanation:

In option A, you are selecting 2 beads from a jar containing 9 beads. To find the number of possible outcomes, you can use the combination formula
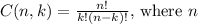`\(C(n, k) = (n!)/(k!(n-k)!)\), where \(n\)` is the total number of items and
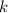`\(k\)` is the number of items to choose. In this case,
`\(C(9, 2) = (9!)/(2!(9-2)!)\),` which simplifies to
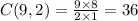`\(C(9, 2) = (9 * 8)/(2 * 1) = 36\)`. Therefore, there are 36 possible outcomes for choosing 2 beads from a jar of 9 beads.

Comparatively, options B, C, and D involve choosing 4 cards out of 8, choosing 5 people out of 6, and choosing 4 socks out of 32, respectively. The combinations for these options are
`\(C(8, 4) = 70\), \(C(6, 5) = 6\)`, and
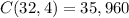`\(C(32, 4) = 35,960\)`. These calculations reveal that options B, C, and D have significantly more possible outcomes than option A, making option A the situation with the fewest number of outcomes.

Therefore, the choice of selecting 2 beads from a jar of 9 beads in option A gives the fewest number of possible outcomes among the given scenarios.