Question

A mass weighting 48 lbs stretches a spring 6 inches. The mass is in a medium that exerts a viscous resistance of 27 lbs when the mass has a velocity of 6 ft/sec. Suppose the object is displaced an additional 6 inches and released.

Required:
a. Find an equation for the object's displacement, u(t), in feet after t seconds.
b. What is the mass of the object?
c. What is the damping coefficient?
d. What is the spring constant?

Answer 1

a)

`u(t)=0.499ft.e^{-(144.76lb/s)/(2(48lb))t}cos(\omega t)\\\\u(t)=0.499ft.e^(-1.5t)cos(\omega t)`

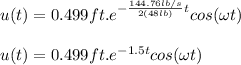
b)

m = 48lb

c)

b = 144.76lb

Step-by-step explanation:

The general equation of a damping oscillate motion is given by:

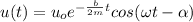`u(t)=u_oe^{-(b)/(2m)t}cos(\omega t-\alpha)` (1)

uo: initial position

m: mass of the block

b: damping coefficient

w: angular frequency

α: initial phase

a. With the information given in the statement you replace the values of the parameters in (1). But first, you calculate the constant b by using the information about the viscous resistance force:

`|F_(vis)|=bv\\\\b=(|F_(vis)|)/(v)\\\\|F_(vis)|=27lbs=27*32.17ft.lb/s^2=868.59ft.lb/s^2\\\\b=(868.59)/(6)lb/s=144.76lb/s`

Then, you obtain by replacing in (1):

6in = 0.499 ft

`u(t)=0.499ft.e^{-(144.76lb/s)/(2(48lb))t}cos(\omega t)\\\\u(t)=0.499ft.e^(-1.5t)cos(\omega t)`

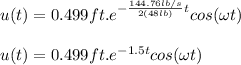
b.

mass, m = 48lb

c.

b = 144.76 lb/s