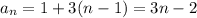1 Answer

Stewe · Answer 1 · 2021-03-04T22:47:52+0000

If the pattern continues, so that each term is separated by a distance of 3, then the sequence is given by the recursive rule

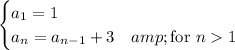
$\begin{cases}a_1=1\\a_n=a_(n-1)+3&\text{for }n>1\end{cases}$

From this definition, we can write
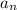a_n in terms of
a_1 :

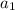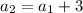
a_2=a_1+3

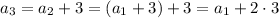
$a_3=a_2+3=(a_1+3)+3=a_1+2\cdot3$

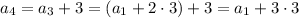
$a_4=a_3+3=(a_1+2\cdot3)+3=a_1+3\cdot3$

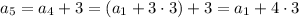
$a_5=a_4+3=(a_1+3\cdot3)+3=a_1+4\cdot3$

and so on, up to

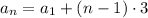
$a_n=a_1+(n-1)\cdot3$

(notice how the subscript on a and coefficient on 3 add up to n)

or

a_n=1+3(n-1)=3n-2

Please log in or register to add a comment.