Question

For a large supermarket chain in a particularâ state, aâ women's group claimed that female employees were passed over for management training in favor of their male colleagues. The company denied thisâ claim, saying it picked the employees from the eligible pool at random to receive this training.â Statewide, the large pool of more than 100 eligible employees who can be tapped for management training is 40â% female and 60â% male. Since this programâ began, 35 of the 50 employees chosen for management training were male and 15 were female.

Complete parts (a) and (b).
(a) Is there sufficient evidence to support the women's claim?
(b) Compute a 95% confidence interval and write your conclusions.

Answer 1

1) As the P-value (0.097) is greater than the significance level (0.05), the effect is not significant.

The null hypothesis failed to be rejected.

There is not enough evidence to support the women's claim that female employees were passed over for management training in favor of their male colleagues.

2) The 95% confidence interval for the population proportion is (0.173, 0.427).

The populations proportion (π=0.4) is included in this confidence interval, so the claim has no enough evidence to be supported.

Explanation:

This is a hypothesis test for a proportion.

The claim is that female employees were passed over for management training in favor of their male colleagues.

We use the women's part for sample and population proportions.

Then, the null and alternative hypothesis are:

`H_0: \pi=0.4\\\\H_a:\pi<0.4`

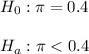
The significance level is 0.05.

The sample has a size n=50 persons.

The sample proportion is p=0.3.

`p=X/n=15/50=0.3`

The standard error of the proportion is:

`\sigma_p=\sqrt{(\pi(1-\pi))/(n)}=\sqrt{(0.4*0.6)/(50)}\\\\\\ \sigma_p=√(0.0048)=0.069`

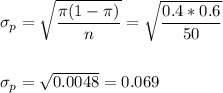
Then, we can calculate the z-statistic as:

`z=(p-\pi+0.5/n)/(\sigma_p)=(0.3-0.4+0.5/50)/(0.069)=(-0.09)/(0.069)=-1.299`

This test is a left-tailed test, so the P-value for this test is calculated as:

`\text{P-value}=P(z<-1.299)=0.097`

As the P-value (0.097) is greater than the significance level (0.05), the effect is not significant.

The null hypothesis failed to be rejected.

There is not enough evidence to support the claim that female employees were passed over for management training in favor of their male colleagues.

b) We have to calculate a 95% confidence interval for the proportion.

The sample proportion is p=0.3.

The standard error of the proportion is:

`\sigma_p=\sqrt{(p(1-p))/(n)}=\sqrt{(0.3*0.7)/(50)}\\\\\\ \sigma_p=√(0.0042)=0.0648`

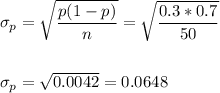
The critical z-value for a 95% confidence interval is z=1.96.

The margin of error (MOE) can be calculated as:

`MOE=z\cdot \sigma_p=1.96 \cdot 0.0648=0.127`

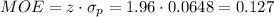
Then, the lower and upper bounds of the confidence interval are:

`LL=p-z \cdot \sigma_p = 0.3-0.127=0.173\\\\UL=p+z \cdot \sigma_p = 0.3+0.127=0.427`

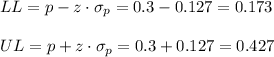
The 95% confidence interval for the population proportion is (0.173, 0.427).

The populations proportion (π=0.4) is included in this confidence interval, so the claim has no enough evidence to be supported.