Question

Can someone please help? :((

if you want another 50 points or more you could maybe help with one of the previous unanswered questions on my profile

Answer 1

Just find the vertex and then compare with graph

#a

• y=2x²-8
• y=2(x-0)²-8

Parabola opening upwards

• Vertex at (0,-8)

Graph 3

#2

• y=(x+3)²+0

Vertex at (-3,0)

Graph IV

#3

• y=-2(x-4)²+8

Parabola opening downwards as a is -ve

Graph I

#4

One graph is left

• Graph Ii

Answer 2

a) graph iii)

b) graph iv)

c) graph i)

d) graph ii)

Explanation:

Vertex form of a quadratic equation:
`y = a(x - h)^2 + k`

where
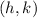`(h, k)` is the vertex (turning point)

First, determine the vertices of the parabolas by inspection of the graphs:

• Graph i) → vertex = (4, 8)
• Graph ii) → vertex = (3, -8)
• Graph iii) → vertex = (0, -8)
• Graph iv) → vertex = (-3, 0)

Next, write each given equation in vertex form and compare to the vertices above.

`\textsf{a)}\quad y=2x^2-8`

`\textsf{Vertex form}: \quad y=2(x-0)^2-8`

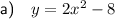
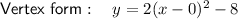
⇒ Vertex = (0, -8)

Therefore, graph iii)

`\textsf{b)} \quad y=(x+3)^2`

`\textsf{Vertex form}: \quad y=(x+3)^2+0`

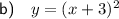
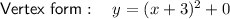
⇒ Vertex = (-3, 0)

Therefore, graph iv)

`\textsf{c)} \quad y=-2|x-4|^2+8`

`\textsf{Vertex form}: \quad y=-2|x-4|^2+8`

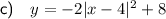
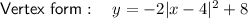
⇒ Vertex = (4, 8)

Therefore, graph i)

`\textsf{d)} \quad y=(x-3)^2-8`

`\textsf{Vertex form}: \quad y=(x-3)^2-8`

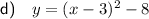
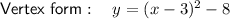
⇒ Vertex = (3, -8)

Therefore, graph ii)