Question

The value of a certain car decreases by 16% each year. What is the 1⁄2-life of the car?

Answer 1

The half life of the car is 3.98 years.

Explanation:

The value of the car after t years is given by the following equation:

`V(t) = V(0)(1-r)^(t)`

In which V(0) is the initial value and r is the constant decay rate, as a decimal.

The value of a certain car decreases by 16% each year.

This means that
`r = 0.16`

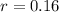
So

`V(t) = V(0)(1-r)^(t)`

`V(t) = V(0)(1-0.16)^(t)`

`V(t) = V(0)(0.84)^(t)`

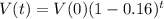
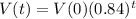
What is the 1⁄2-life of the car?

This is t for which V(t) = 0.5V(0). So

`V(t) = V(0)(0.84)^(t)`

`0.5V(0) = V(0)(0.84)^(t)`

`(0.84)^(t) = 0.5`

`\log{(0.84)^(t)} = \log{0.5}`

`t\log{0.84} = \log{0.5}`

`t = \frac{\log{0.5}}{\log{0.84}}`

`t = 3.98`

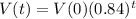
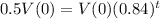
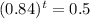
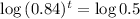
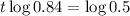
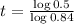
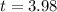
The half life of the car is 3.98 years.