Question

Mr. Ray wanted to measure the height of a light post. He placed a mirror on the ground 32 feet from the light post, then walked backwards until he was able to see the top of the light post. His eyes were 6 feet above the ground and he was 9 feet from the mirror. Using similar triangles, find the height of the light post to the nearest tenth of a foot.

Answer 1

Option (2) is the answer.

Explanation:

From the figure attached,

AB represents the length of Mr. Ray, ED represents the light post and the mirror was placed at point C.

Here AB = d = 6 feet

CD = w = 32 feet

BC = f = 9 feet

Since both the triangles ABC and EDC are similar, their corresponding sides will be in the same ratio.

`(AB)/(DE)=(BC)/(CD)`

`(6)/(h)=(9)/(32)`

h =
`(6* 32)/(9)`

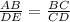
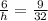
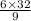
h = 21.33 feet

h ≈ 21.3 feet

Therefore, height of the light post is 21.3 feet.

Option (2) is the answer.