Answer:
(a) The probability of the company becoming a successfully approved supplier to Ford Motor Company is 0.2048.
(b) The probability of the company becoming a successfully approved supplier to General Motors Company is 0.2448.
Explanation:
A local startup company working on a smart dashboard camera system is bidding to be a supplier for both Ford Motor company and General Motors.
Both the companies have a two-tier system where suppliers are approved in two separate phases.
It is provided that a company can move on to Phase II if they have passed the Phase I phase.
(a)
The chances of landing with a supplier contract with Ford Motor Company is 32% in Phase I while it is 64% in Phase II.
That is:
P (Phase I) = 0.32
P (Phase II | Phase I) = 0.64
Consider the tree diagram below.
Compute the probability of the company becoming a successfully approved supplier to Ford Motor Company as follows:
P (Supplier to Ford Motor Company) = P (Phase II | Phase I) × P (Phase I)
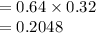
Thus, the probability of the company becoming a successfully approved supplier to Ford Motor Company is 0.2048.
(b)
The chances of landing with a supplier contract with General Motors is 68% for Phase I and 36% for Phase II.
That is:
P (Phase I) = 0.68
P (Phase II | Phase I) = 0.36
Consider the tree diagram below.
Compute the probability of the company becoming a successfully approved supplier to General Motors as follows:
P (Supplier to General Motors Company) = P (Phase II | Phase I) × P (Phase I)
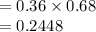
Thus, the probability of the company becoming a successfully approved supplier to General Motors Company is 0.2448.