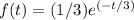Question

A device that continuously measures and records seismic activity is placed in a remote region. The time, T, to failure of this device is exponentially distributed with mean 3 years. Since the device will not be monitored during its first two years of service, the time to discovery of its failure is X = max(T, 2).

Answer 1

E[X]=
`2 + 3 e^{(-2/3)`

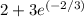
Explanation:

The objective of this question is to determine E[X].

T is defined (0,infinity)

X=max(c,T)

where; c=constant

E[X]=c+function (c,infinity) Sf(t)dt

E[X] =
`e^{-t/3`

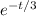
E[X]=2+function (2,infinity)
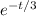`e^{-t/3`dt

E[X] =
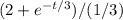`(2+e^(-t/3))/(1/3)` function (2,infinity)

E[X]=
`2 + 3 e^{(-2/3)`

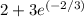
If X = T if T ≥ 2 and X = 2 if 0 ≤ T < 2,

So Since T is exponentially distributed with mean 3, the density function of T is
`f(t) = (1/3)e^{(-t/3)`