Answer:
440 square units
Explanation:
We can find half of a side of the pentagon with the expression
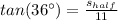
Because, as a regular polygon, all its sectors have the same central angle, and the apothem divides equally each sector in two equal parts.
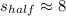
Therefore, half of a side is 8 units long, which means each side measures 16 units.
Now, the area of a penthagon is defined by
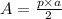
Where
 is the perimeter and
is the perimeter and
 is the apothem. Where the perimeter is the sum of all sides, which is 80 units.
is the apothem. Where the perimeter is the sum of all sides, which is 80 units.
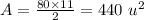
Therefore, the right answer is the second choice.