Question

What is the determinant of the coefficient matrix of the system

Answer 1

130

Explanation:

We are given the following system of equations

`4x+3y+2z=0\\-3x+y+5z=0\\-x-4y+3z=0`

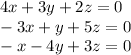
From this system, we can create the following coefficient matrix

`\left[\begin{array}{ccc}4&3&2\\-3&1&5\\-1&-4&3\end{array}\right]`

Let us go over a method of finding the determinant of a 3x3 matrix real quick.

`\left[\begin{array}{ccc}a&b&c\\d&e&f\\h&i&j\end{array}\right]`

If this is our 3x3 matrix, the determinant will be as follows

`a*det(\left[\begin{array}{ccc}e&f\\i&j\\\end{array}\right]) -b*det(\left[\begin{array}{ccc}d&f\\h&j\\\end{array}\right]) +c*det(\left[\begin{array}{ccc}d&e\\h&i\\\end{array}\right] )`

Which is the same thing as

`a(ej-fi)-b(dj-fh)+c(di-eh)`

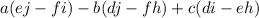
Now back to our original system

`\left[\begin{array}{ccc}4&3&2\\-3&1&5\\-1&-4&3\end{array}\right]`

Using this same formula, we can find the determinant

`4*([1*3]-[-4*5])-3([-3*3]-[-1*5])+2([-3*(-4)]-[-1*1])\\\\4(3+20)-3(-9+5)+2(12+1)\\\\4(23)-3(-4)+2(13)\\\\92+12+26=130`