Question

Exercise 3 A pipe discharges wine into a 1.5-m-diameter tank. Another pipe (15 cm diameter), located near the base of the tank, is used to discharge wine out of the tank. Calculate the volumetric flow rate into the tank if the wine level remains constant at 2.5 m.

Answer 1

Volume flow rate, Q, into the tank is 12.376 m³

Explanation:

Here we have Bernoulli's equation presented as follows

`(P_(1))/(\rho _(1)g)+(v_(1)^(2))/(2g) + z_(1) = (P_(2))/(\rho _(2)g)+(v_(2)^(2))/(2g) + z_(2)`

Where:

P₁ = Pressure, of the open tank = Atmospheric pressure = 0

P₂ - Pressure at the discharge of the pipe = Atmospheric pressure = 0

ρ₁ = Density of the fluid = ρ₂

v₁ = Velocity of the fluid in the tank

v₂ = Velocity of the fluid in the pipe

d₁ = Diameter of the tank = 1.5 m

d₂ = Diameter of the pipe = 15 cm = 0.15 m

A₁ = Cross sectional area of tank = π×d₁²/4 = 1.767 m²

A₂ = Cross sectional area of pipe= π×d₂²/4 = 0.01767 m²

z₁ = Level of water in the tank = 0 m

z₂ = Level of water in the pipe = 2.5 m

Whereby the level remains constant at 2.5 m, pressure at the base, P₂ = ρ₁×g×2.5

Also

v₁×A₁ = v₂×A₂ which gives;

v₁×1.767 = v₂×0.01767

v₂ = v₁×1.767/0.01767 = 100·v₁

Hence we have;

`(0)/(\rho _(1)g)+(v_(1)^(2))/(2g) + z_(1) = (0)/(\rho _(1)g)+((100v_(1))^(2))/(2g) + z_(2)`

`z_(1) - z_(2) = ((100v_(1))^(2))/(2g)- (v_(1)^(2))/(2g)`

`(2.5)2g = 99v_(1)^(2)}`

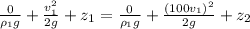
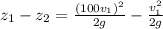
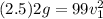
v₁² = 2.5×2×9.81 = 49.05

v₁ = √49.05 = 7.0035 m/s

Therefore, since the rate of discharge = Rate of entry into the tank, we have;

Volume flow rate, Q, into the tank = v₁×A₁ = 7.0035 m/s × 1.767 m² = 12.376 m³.