Question

Solve the right triangle, AABC, for the missing side and angles to the nearest

tenth given sides a = 14.9 and b = 17.5.

Answer 1

The missing side is 22.98, or rounded to the nearest tenth, 23

The angles are 90, 40.37, and 49.63

Explanation:

We can use the Pythagorean theorem to solve this problem;

`a^2 + b^2 = c^2`

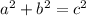
Since a = 14.9 and b= 17.5, we need to find the missing side, or c

`14.9^2 + 17.5 ^2 = c^2`

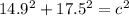
Using a calculator this gives us;

528.26 =
`c^2`

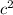
Now to undo
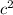`c^2`, we have to square root both sides

`√(528.26) = √(c^2)`

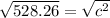
22.98 = c

Now to round to the nearest tenth, we know that .9 is greater than 5, so we can round 22.98 to 23

Now to find the angles.

We know that the triangle has a hypotenuse of 23, a short side of 14.9 and a long side of 17.5.

I labeled the side opposite of 14.9, x, and I will use sin to solve for the angle.

We know that sin= opposite/hypotenuse

So, sin(x)=14.9/23

Since we want to find the angle we must use the inverse of the trig function.

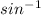`sin^-^1`(14.9/23) = x

By using a calculator we get

x=40.37

Now since we know that this is a right triangle, we have a 90 degree angle.

So, we can subtract from 180 to find the third angle.

180-90-40.37=49.63

The angles of the triangle are 90, 40.37 and 49.63.

Hope this helped let me know if this can be explained further or if anything is wrong! : )