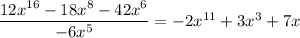Answer:
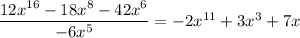
Explanation:
Replace the questions marks with letters:
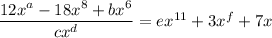

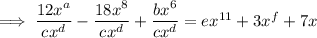
Taking the second term and calculating the coefficient of the denominator:
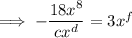
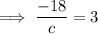
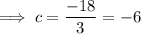
Taking the first term, substituting the found coefficient of the denominator and calculating the coefficient e:


Taking the third term, substituting the found coefficient of the denominator, and calculating the coefficient of the numerator and the exponent:
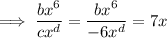
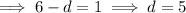
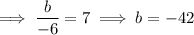
Taking the first term, substituting the found coefficient and exponent of the denominator and the found coefficient e, and calculating the exponent of the numerator::
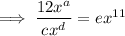
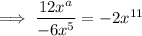
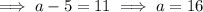
Taking the second term, substituting the found coefficient and exponent of the denominator, and calculating the exponent f:
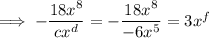
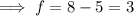
Substituting all found letters: