Question

. Can we conclude that the mean maximum voluntary ventilation value for apparently healthy college seniors is not 110 liters per minute? A sample of 20 yielded the following values

Answer 1

Explanation:

Hello!

Full text:

Can we conclude that the mean maximum voluntary ventilation value for apparently healthy college seniors is not 110 liters per minute ? A sample of 20 yields the following values :

132, 33, 91, 108, 67, 169, 54, 203, 190, 133, 96, 30, 187, 21, 63, 166, 84, 110, 157, 138

Let α= 0.01 What assumptions are necessary ?

The variable of interest is

X: maximum voluntary ventilation value for an apparently healthy college senior.

X[bar]= 111.60

S= 56.30

The parameter to study is the population mean μ, to be able to study the condition to be met is that the population has a normal or at least approximately normal distribution, if this checks, you can apply a one sample t-test to test the claim that the maximum mean value is not 110 Lt/min.

The hypotheses are:

H₀: μ = 110

H₁: μ ≠ 110

α:0.01

`t= (X[bar]-Mu)/((S)/(√(n) ) ) ~~t_(n-1)`

This test is two-tailed, which means that you'll reject the null hypothesis to low or high values of the statistic. Using the critical value approach, the rejection region is divided in two tails determined by two critical values:

`t_(n-1;\alpha /2)= t_(19;0.005)= -2.845`

`t_(n-1;1-\alpha /2)= t_(19;0.995)= 2.845`

`t_(H_0)= (111.60-110)/((56.30)/(√(20) ) ) = 0.13`

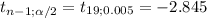
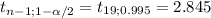
As you see the value of the statistic under the null hypothesis is within the acceptance region, so the decision is to not reject the null hypothesis.

Using the p-value approach, the p-value for this test is 0.9002, this value is greater than the level of significance, so the decision using this approach is to not reject the null hypothesis.

I hope this helps!