Question

The picture shows a cement bag of weight Fg hanging from a rope which itself is supported by two other ropes attached to a ceiling. The latter two ropes make an angle θ1 and θ2 with the ceiling. Determine the tension in each rope. Use the angle addition identity to simplify your result: sin(α ± β) = sin α cos β ± cos α sin β

Answer 1

`T_1= (F_gcos \theta_2)/(sin (\theta_1+\theta_2))`

Explanation:

From the free body diagram attached below; we will see that

T₃ = Fg ------ (1)

Thus; as the system is in equilibrium, the net force in the x and y direction shows to be zero

Then;

`\sum F_x= 0 \to T_2 Cos \theta _2 - T_1 cos \theta _1`

`T_2 Cos \theta _2 = T_1 cos \theta _1 \ \ \ \ \ - - - (2)`

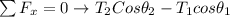
Also;

`\sum F_y =0 \to T_2sin \theta_2+T_1sin \theta_1 - T_3 = 0`

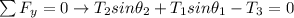
`T_3 = T_2sin \theta_2+T_1sin \theta_1` ---- (3)

From equation (2):

`T_2 = (T_1cos \theta_1)/(cos \theta_2)`

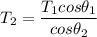
Replacing the above value for T₂ into equation 3; we have

`T_3 = (T_1cos \theta_1)/(cos \theta_2)sin \theta_2+T_1sin \theta_1`

`T_3 cos \theta_2 = {T_1cos \theta_1}{}sin \theta_2+T_1sin \theta_1 cos \theta_2`

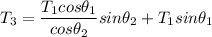
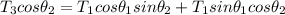
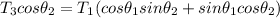`T_3 cos \theta_2 = T_1(cos \theta_1 sin \theta_2+sin \theta_1 cos \theta_2)` ---- (4)

Using trigonometric identity Sin (A+B) = SIn A cos B + Cos A sin B

So ; equation 4 can now be:

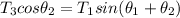`T_3 cos \theta_2 = T_1sin(\theta _1 + \theta_2)` --- (5)

replacing equation (1) into equation (5) ; we have:

`F_g}cos \theta_2 =T_1 sin (\theta_1+\theta_2)`

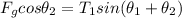
Hence; the tension in the string is:

`T_1= (F_gcos \theta_2)/(sin (\theta_1+\theta_2))`