Question

The tops of two poles, of heights 25m and 35m are connected by a wire which makes and angle of elevation 30 degrees at the top of 25m pole. Find the length of the wire

Answer 1

20m

Explanation:

Given:

Height of pole 1 = 25 m

Height of pole 2 = 35 m

Angle of elevation = 30°

A wire makes an angle of elevation 30° at the top of the 25m pole. From the diagram we can see that AD is the length of the wire.

That means we are to solve for AD.

Taking triangle ADE, we have:

`Sin 30 = (DE)/(AD)`

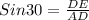
Let's make AD subject of the formula:

`AD = (DE)/(sin30)`

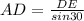
Where DE is the height difference between pole1 and pole 2

= 35 - 25 = 10m

Substituting figures, we have:

`AD = (10)/(sin30)`

AD = 20

Therefore the length of wire is 20m

Answer 2

20 meters

Explanation:

Let the height of the short pole be AB, AB=25cm

Let the height of the tall pole be CE, CE=35cm

In the diagram,

`AB \cong DE $(Opposite sides of a rectangle)\\Therefore: CD=CE-AB\\=35-25=10 meters`

We want to determine the length of the pole connecting the two poles, l.

From right triangle BCD

`sin 30 = (10)/(l) \\$Cross multiplyl sin 30=10\\Divide both sides by sin 30^\circ\\l=10/ sin 30^\circ\\$Length of the wire, l=20m`