Question

The instantaneous speed of a particle moving along one straight line is v(t) = ate−6t, where the speed v is measured in meters per second, the time t is measured in seconds, and the magnitude of the constant a is measured in meters per second squared. What is its maximum speed, expressed as a multiple of a? (Do not include units in your answer.)

Answer 1

v_max = (1/6)e^-1 a

Step-by-step explanation:

You have the following equation for the instantaneous speed of a particle:

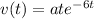`v(t)=ate^(-6t)` (1)

To find the expression for the maximum speed in terms of the acceleration "a", you first derivative v(t) respect to time t:

`(dv(t))/(dt)=(d)/(dt)[ate^(-6t)]=a[(1)e^(-6t)+t(e^(-6t)(-6))]` (2)

where you have use the derivative of a product.

Next, you equal the expression (2) to zero in order to calculate t:

`a[(1)e^(-6t)-6te^(-6t)]=0\\\\1-6t=0\\\\t=(1)/(6)`

For t = 1/6 you obtain the maximum speed.

Then, you replace that value of t in the expression (1):

`v_(max)=a((1)/(6))e^{-6((1)/(6))}=(e^(-1))/(6)a`

hence, the maximum speed is v_max = ((1/6)e^-1)a